1. Условие.
Для ускорения шахматной партии Дима (белые) и Петя (чёрные) решили, что будут каждый раз делать по два хода подряд (а остальные правила не отличаются от правил обычных шахмат). Имеет ли Петя шансы на победу при безошибочной игре Димы?
Решение.
Пусть у чёрных есть выигрышная стратегия. Белые могут передать ход, не меняя позиции (см. рис.), и уже фактически играть чёрными, а, значит, и у них есть выигрышная стратегия. Но у обоих игроков не может быть выигрышной стратегии. Противоречие.

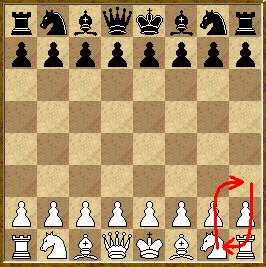
Ответ: нет.
Эта задача несложная, но с помощью похожей идеи можно решить, например, такую задачу (уже несвязанную с шахматной доской):
(Всесоюзная олимпиада школьников, 1987 г., 9 класс) Два игрока поочерёдно выписывают на доске натуральные числа, не превосходящие p. Правилами игры запрещается писать на доске делители уже выписанных чисел. Проигрывает игрок, который не может сделать очередной ход. Выяснить, кто из игроков имеет выигрышную стратегию.
Решение.
Рассмотрим новую игру – с теми же правилами, но нельзя выписывать 1. Если в новой игре у начинающего есть выигрышная стратегия, то она годится и в исходной игре. Если же в новой игре у начинающего выигрышной стратегии нет, то первый игрок в исходной игре может первым ходом написать 1 и тем самым превратить исходною игру в новую с той лишь разницей, что в этой новой игре начинающим будет второй игрок, у которого не будет выигрышной стратегии. Отсюда в исходной игре выигрышную стратегию имеет первый игрок.
Ответ: первый игрок.


2. Условие.
Сколькими способами можно расставить 8 ладей на чёрных полях шахматной доски так, чтобы они не били друг друга?
Решение.
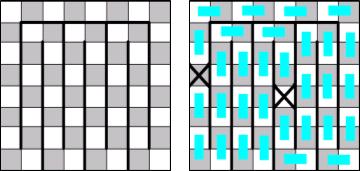
Если не выдвигать ограничений на цвет полей, то для доски nхn число способов расстановки n ладей так, чтобы они не били друг друга, равно n!. Раскрасим чёрные поля доски в два цвета: красный и синий (см. рис.). 4 ладьи окажутся на красных полях, 4 – на синих. Красные и синие поля образуют как бы отдельные доски 4x4, поэтому число способов расстановки 4 ладей, как на красных, так и на синих полях равно 4!. Отсюда число способов расстановки 8 ладей на чёрных полях шахматной доски равно 4!².

Ответ: 4!².


3. Условие.
На доске 9x9 закрашено несколько клеток так, что от любой закрашенной клетки можно добраться до любой другой, двигаясь только по закрашенным клеткам и каждый раз переходя на соседнюю клетку через сторону. Какой наибольший периметр может быть у закрашенной фигуры?
Решение.
Докажем вначале лемму.
Лемма. Периметр связной фигуры из n клеток не превосходит 2n+2.
Доказательство леммы.
Пусть k – число “перегородок” между клетками фигуры. Тогда периметр фигуры равен 4n–2k (т.к. он равен разности суммы периметров всех клеток, из которых состоит фигура, (4n) и удвоенного (т.к. каждая “перегородка” входит в две клетки) числа “перегородок” (2k)). Рассмотрим граф, вершинами которого являются закрашенные клетки, а рёбра соединяют клетки, имеющие общую сторону. В этом графе n вершин и k рёбер. Граф связный, поэтому k≥n–1. Отсюда периметр фигуры P=4n–2k≤4n–2(n–1)=2n+2.
Лемма доказана.
Если фигура состоит из 59 или менее клеток, то её периметр не больше 2∙59+2=120. Если из 60 или более, то рассмотрим фигуру состоящую из незакрашенных клеток. В ней не более 81–60=21 клеток, поэтому её периметр не превосходит 4∙21=84. Каждый отрезок периметра закрашенной фигуры принадлежит либо периметру фигуры, состоящей из незакрашенных клеток, либо периметру всего квадрата 9x9 (его периметр 4∙9=36), поэтому и в этом случае периметр закрашенной фигуры не больше 84+36=120. Осталось заметить, что периметр закрашенной фигуры может быть равным 120 (см. рис.).

Ответ: 120.


4. Условие.
Расставить на доске 8x8 наименьшее возможное число коней так, чтобы каждое поле доски было бито (поле, на котором конь стоит, является битым).
Решение.
12 коней (пример на рисунке). Меньше 12 не хватит, т.к. каждое из 12 красных полей (см. рис.) бьют разные кони.

Ответ: 12 коней.


5. Условие.
Какое наибольшее число ладей можно расставить на доске m n так, чтобы каждая била не более двух других?
Решение.
Посчитаем общее число ладей, которых бьёт ладья, обходящая доску по периметру (см. левый рисунок). Их не более чем 2(m+n). При этом каждую из стоящих на доске ладей мы посчитали по крайней мере дважды. Поэтому число ладей на доске не более m+n. Пример расстановки m+n ладей показан на правом рисунке.

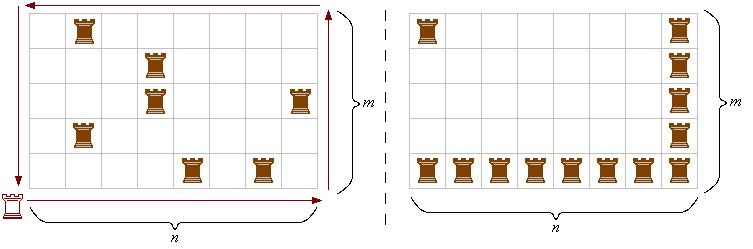
Ответ: m+n.


6. Условие.
Можно ли доску 4xn обойти конём, побывав на каждом поле ровно 1 раз, и последним ходом вернуться на исходное поле?
Решение.
Раскрасим доску в 4 цвета (см. рис).

С синих полей можно попасть только на красные, с зелёных – только на жёлтые. Синих клеток столько же, сколько красных. Попав на красное поле, конь должен пойти на синее, иначе, если он пойдёт на жёлтое, в обходе коня красные поля встретятся чаще, чем синие. Аналогично, попав на синее поле, конь должен пойти на красное. Но тогда конь будет ходить только по синим и красным полям, что невозможно.
Ответ: Нет.


7. Условие.
а) На доске 10x10 рассматривается фигура “лев”, которая ходит на одну клетку вправо, вниз или по диагонали влево-вверх. Может ли “лев” обойти по одному разу все клетки доски и вернуться на исходное поле? б) А если “лев” возвращается на поле, соседнее от исходного (справа или слева)?
Решение.
а) Для возвращения в исходную точку “лев” должен сделать одинаковое число вниз, вправо и влево-вверх, т. е. всего сделать число ходов, делящееся на 3. Но чтобы “льву” побывать в каждой из 100 клеток доски и вернуться на исходное поле, ему придётся сделать 100 ходов, а 100 не делится на 3.
б) Разность номеров столбца и строки при каждом ходе либо уменьшается на 2, либо увеличивается на 1. Значит, её остаток по модулю 3 каждый раз увеличивается на 1. Так как всего ходов 99, этот остаток не изменился, но разность в конце отличается от исходной на 1. Противоречие. Значит, такого обхода нет.
Ответ: не может.


8. Условие.
Из доски 8x8 выпилили 2 поля. В каких случаях оставшиеся клетки можно разбить на 31 прямоугольник 1x2?
Решение.
Если вырезанные клетки одного цвета, то останется на доске неравное количество белых и чёрных клеток, а каждый прямоугольник 1x2 содержит поровну чёрных и белых клеток. Значит, оставшуюся часть доски разрезать на прямоугольники 1x2 нельзя.
Если вырезанные клетки разного цвета, то можно. Достаточно найти маршрут обхода доски по клеткам (см. рис). Теперь при вырезании двух клеток каждую из образовавшихся цепей легко разрезать на прямоугольники 1x2 (напр. см. рис.).

Ответ: Если вырезанные клетки разного цвета.


9. Условие.
Можно ли из шахматной доски 8x8 выкинуть а) 32, б) 48 клеток так, чтобы на оставшихся клетках нельзя было разместить доминошку 1x2, но при добавлении любой из выкинутых клеток доминошку расположить было бы можно?
Решение.
а) Можно, например, выкинуть все чёрные клетки.
б) Можно (см. рис., серым обозначены оставшиеся клетки, белым – выкинутые).

На самом деле 48 – наибольшее число клеток, которые можно выкинуть подобным образом, но доказательство этого факта слишком скучное (надо заметить, что если мы разобьём доску на 16 квадратов 2x2, то при выбрасывании 49 или более клеток в одном из таких квадратов не останется клеток (назовём такой квадрат “пустым”); далее надо рассматривать три случая расположения пустого квадрата…).
Ответ: можно.


10. Условие.
Доска mxn разбита на доминошки. Можно ли её клетки раскрасить в два цвета так, чтобы любая доминошка в данном разбиении содержала клетки разных цветов, но в любом другом разбиении этой доски на доминошки нашлась бы доминошка, содержащая две клетки одного цвета?
Решение.
Например, можно у вертикальных доминошек покрасить в чёрный цвет нижнюю клетку, а у горизонтальных – левую, остальные клетки покрасить в белый цвет. Введём систему координат, в которой координаты центров клеток целочисленны, а оси направлены вверх и вправо. Пусть S – разность суммы координат центров всех белых клеток и суммы координат центров всех чёрных. В исходной расстановке каждая доминошка вносит в эту сумму вклад равный +1, поэтому S равно количеству доминошек. Допустим, что у нас есть какое-то другое разбиение, в котором каждая доминошка содержит по одной чёрной и одной белой клетке построенной раскраски. Так как S зависит только от раскраски, а вклад каждой доминошки нового разбиения не превосходит +1, мы заключаем, что все вклады равны +1, то есть в каждой доминошке нового разбиения чёрная клетка тоже находится слева или снизу. Теперь, если будем восстанавливать доминошки так, чтобы доминошки содержали клетки обоих цветов, причём в каждой доминошке чёрная клетка была бы слева или снизу, двигаясь вначале по первой вертикали снизу вверх, потом по второй снизу вверх и т. д. получим разбиение, которое было.
Ответ: можно.


11. Условие.
На шахматной доске 9x9 расставлены 9 ладей, не бьющих друг друга. Каждую из этих ладей передвинули ходом коня. Докажите, что теперь какие-то две ладьи бьют друг друга.
Решение.
Для каждой ладьи выпишем номер строки и номер столбца, в которых она стоит, после чего сложим все выписанные числа. Если ладьи не бьют друг друга, то получаемая сумма равна 2∙(1+2+…+9) независимо от расстановки, т. к. все номера строк и столбцов выписаны по одному разу. При ходе конём сумма номеров строки и столбца для каждой ладьи меняется либо на 1, либо на 3, то есть на нечётное число. Поскольку ладей всего 9, общая сумма изменится на нечётное число. Таким образом, эта сумма не может остаться прежней, так что ладьи не могут снова оказаться не бьющими друг друга.