12. Условие.
Из доски 2005x2005 произвольным образом вырезали 1 клетку. Можно ли оставшиеся клетки разбить на трёхклеточные уголки? А если клетку вырезали из доски 2²⁰⁰⁵x2²⁰⁰⁵?
Решение.
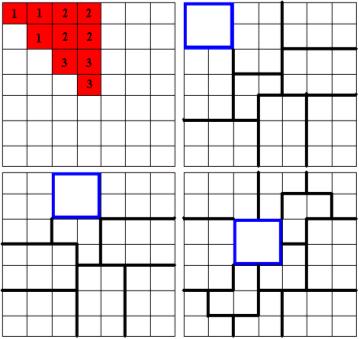
Выброшенная клетка лежит в одном из квадратов (2005–6)x(2005–6), примыкающих к углам доски. Клетки вне этого квадрата легко разобьём уголки. Для нового квадрата (2005–6)x(2005–6) выброшенная клетка лежит в одном из квадратов (2005–6∙2)x(2005–6∙2), примыкающих к углам доски. Клетки вне этого квадрата легко разобьём на уголки. Будем продолжать такую процедуру, пока не останется не разбитым на уголки лишь квадрат 7x7 с где-то вырезанной клеткой. С точностью до симметрии и поворотов этого квадрата в нём вырезана одна из красных клеток (см. рис. в правом нижнем углу). Теперь в зависимости от того, из какого синего квадрата была вырезана клетка, выберем соответственный способ разбиения квадрата 7x7 на уголки (см. рис. в правом нижнем углу, прямоугольники 2x3 разбиваются на уголки, синий квадрат без вырезанной клетки образует уголок).

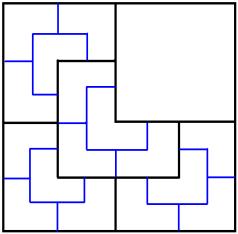
Для квадрата 2²⁰⁰⁵x2²⁰⁰⁵ используем ту же идею, учитывая следующее разбиение:

Ответ: можно.


13. Условие.
Докажите, что число способов разрезать прямоугольник mxn на уголки не превосходит числа способов разрезать прямоугольник 2mx2n на уголки так, что никакие два уголка не образуют прямоугольника 2x3.
Решение.
Пусть есть все разбиения прямоугольника m n на уголки. Каждому из этих разбиений поставим в соответствие разбиение прямоугольника 2mx2n на уголки так, что никакие два уголка не образуют прямоугольника 2x3. Для этого в каждом разбиении прямоугольника mxn на уголки разрежем каждый уголок как показано на рисунке и увеличим получившуюся картинку два раза.

Легко видеть, что получилось разбиение прямоугольника 2mx2n на уголки так, что никакие два уголка не образуют прямоугольника 2x3. Отсюда и следует, что число способов разрезать прямоугольник m n на уголки не превосходит числа способов разрезать прямоугольник 2mx2n на уголки так, что никакие два уголка не образуют прямоугольника 2x3.


14. Условие.
Фишка стоит на поле, соседнем по стороне с угловым, доски nxn. Каждый из двух играющих по очереди передвигает фишку на соседнее по стороне поле. Ходить второй раз на поле, где стояла фишка, нельзя. Проигрывает тот, кому некуда ходить. Кто выиграет при правильной игре?
Решение.
Если n – чётно, разбиваем доску на домино. Теперь, если первый будет ставить фишку на ту доминошку, где перед его ходом стояла фишка, то он добьётся победы. Если n – нечётно, разобьём на домино все клетки, кроме угловой (говоря “угловая” клетка, будем иметь ввиду клетку, рядом с которой стоит фишка), а также покрасим клетки в шахматном порядке так, чтобы угловая клетка была чёрной. Тогда после хода второго фишка будет находиться на белой клетке, т.е. на одной из доминошек. Теперь, если первый будет ставить фишку на ту доминошку, где перед его ходом стояла фишка, то он добьётся победы.
Ответ: первый.


15. Условие.
Ладья, делая ходы по вертикали и горизонтали на соседнее поле, за 64 хода обошла все поля шахматной доски и вернулась на исходное поле. Может ли число её ходов по вертикали равняться числу её ходов по горизонтали?
Решение.
Достаточно доказать, что число горизонтальных ходов ладьи при делении на 4 даёт в остатке 2 (из этого сразу будет следовать, что число горизонтальных ходов не равно 32, а, следовательно, число горизонтальных ходов не равно числу вертикальных ходов).
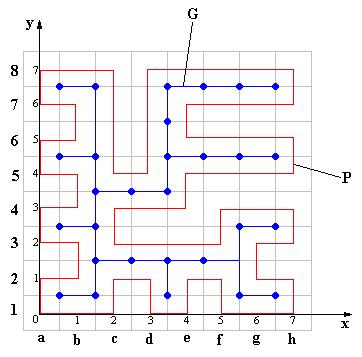
Пусть траектория центра ладьи ограничивает многоугольник Р (мы считаем, что центр ладьи всегда ставится в центр клетки). Та часть разметки шахматной доски на поля, которая находится целиком внутри Р, образует некоторый граф G (см. рис., на рисунке Р выделен красным, G – синим), вершины этого графа – узлы шахматной разметки. Нетрудно понять, что G – дерево. Введём систему координат с началом в центре поля а1 шахматной доски и осями, параллельными горизонталям и вертикалям доски (см. рис.). Тогда все вершины Р имеют целочисленные координаты, а стороны параллельны осям.

Установим следующий факт:
Лемма. Пусть Р – многоугольник с вершинами в целых точках, со сторонами, параллельными осям, такой что соответствующий граф G (получаемый соединением центров соседних клеточек Р) является деревом. Далее, пусть А – число целых точек на границе Р, у которых абсцисса чётная, В – число целых точек на границе Р, у которых абсцисса нечётная. Тогда сумма длин горизонтальных сторон Р сравнима с А–В+2 по модулю 4.
Доказательство леммы проведём индукцией по площади Р. База (площадь Р равна 1, Р состоит из одной клеточки) тривиальна. Переход осуществляем, отрезая от Р клеточку, соответствующую листу дерева G. Клеточка может примыкать к Р по горизонтальному отрезку, либо по вертикальному отрезку. В первом случае сумма длин горизонтальных сторон Р не изменяется, в то же время А–В тоже не изменяется. Во втором случае и сумма длин, и А–В изменяются на 2. Для многоугольника Р, ограниченного траекторией центра ладьи, А=32, В=32, следовательно число горизонтальных ходов ладьи сравнимо с А–В+2=2 по модулю 4.
Ответ: нет.


16. Условие.
Доска 6x6 покрыта без наложений 18 костями домино размером 1x2. Докажите, что доску можно разрезать по вертикали или горизонтали, не повредив ни одной доминошки.
Решение.
Заметим, что если доску нельзя разрезать по какой-то горизонтальной или вертикальной линии, то эта линия пересекает не менее двух доминошек (если бы пересекала только одну доминошку А, то части, на которые эта линия делит доску, без клеток, которые занимает на этих частях доминошка А, состояли бы из нечётного числа клеток, и их нельзя было бы покрыть целым числом доминошек). Всего линий 10. Если предположить, что ни по одной из этих линий доску разрезать нельзя, то получим, что доминошек не менее 20.


17. Условие.
В клетках доски 2005х2005 стоят “+” и “–”. За один ход можно поменять знаки всех клеток одного креста (т. е. объединения некоторой вертикали и некоторой горизонтали). Можно ли добиться того, чтобы во всех клетках доски стояли “+”?
Решение.
Можно. Достаточно показать, что можно изменить знак любой клетки и при этом знаки других клеток оставить прежними. Для этого возьмём крест с центром в клетке, знак которой мы хотим поменять, и для всех клеток этого креста поменяем знаки клеток крестов, центрами которых являются эти клетки.
Ответ: можно.


18. Условие.
В одной не угловой клетке шахматной доски стоит “–”, а в остальных клетках стоят “+”. Разрешается поменять знаки на всех клетках одной вертикали, горизонтали или диагонали. Можно ли с помощью нескольких таких операций добиться того, чтобы на всех клетках доски стояли одинаковые знаки.
Решение.
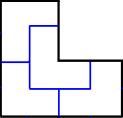
Выделим на доске несколько клеток так, они образовывали фигуру, изображённую на рисунке, и чтобы на одной из этих клеток стоял “–”.

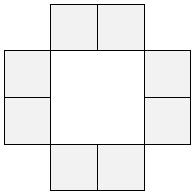
Заметим, что любая из операций, описанных в условии, не меняет чётности числа минусов в нашей фигуре, поэтому в нашей фигуре будет всегда нечётное число минусов, а, значит, в ней будут и “+”, и “–”.
Ответ: нет.


19. Условие.
Дано поле (2n+1)x(2n+1) клеток. Двое по очереди ставят фишки: первый может поставить фишку в клетку (x, y), если в столбце с номером x и строке с номером y до его хода поставлено в сумме чётное число фишек, второй – если нечётное. В каждую клетку можно поставить не более одной фишки. Проигрывает тот, кто не может сделать ход. Докажите, что один из игроков выигрывает, как бы он не играл.
Решение.
Построим граф, в котором вершины – клетки поля, рёбра соединяют клетки одной строки или одного столбца. Если на клетку ставится фишка, то соответствующую этой клетке вершину графа, вместе со всеми рёбрами, выходящими из этой вершины, мы удаляем. Заметим, что условие “в столбце с номером x и строке с номером y поставлено в сумме чётное число фишек” равносильно условию “степень вершины графа, соответствующей клетке (x, y) чётна”. Докажем, что у первого игрока всегда есть ход. Заметим, что перед ходом первого игрока наш граф состоит из нечётного числа вершин, а, значит, в этом графе найдётся вершина, степень которой чётна (иначе бы сумма степеней вершин графа была бы нечётной, что невозможно, т. к. эта сумма равна удвоенному количеству рёбер), на клетку, соответствующую этой вершине, первый и может поставить фишку. Отсюда первый игрок выигрывает, как бы он не играл.


20. Условие.
На всех клетках шахматной доски расставлены натуральные числа. Разрешается выделить любой квадрат размером 3х3 или 4х4 и увеличить все числа в нём на 1. Мы хотим в результате нескольких таких операций добиться, чтобы числа во всех клетках делились на 10. Всегда ли удастся это сделать?
Решение.
Будем рассматривать числа по модулю 10. Возьмём набор, состоящий только из нулей, и подсчитаем, сколько наборов мы сможем получить, исходя из него с помощью указанных в условии операций. На доске 8х8 можно выделить 6²=36 квадратов 3x3 и 5²=25 квадратов 4x4. Поэтому искомых наборов не больше 10²⁵⁺³⁶=10⁶¹. Но всего наборов 10⁶⁴. Значит, существует набор, который с помощью указанных операций из набора, состоящего из нулей, получить не удастся. Если мы примем такой набор за исходный, то набор из нулей из такого набора получить не удастся.
Ответ: нет, не всегда.


21. Условие.
На клетках доски nxn расставили числа 1, 2, …, n² так, что получился магический квадрат (суммы чисел во всех горизонтальных рядах и во всех вертикальных рядах равны). Для всех возможных пар клеток центры этих клеток соединили вектором в направлении от большего числа к меньшему. Чему равна сумма всех полученных векторов?
Решение.
Докажем, что сумма этих векторов равна 0. Достаточно доказать, что сумма S горизонтальных проекций этих векторов равна 0. Примем длину стороны клетки за 1, за положительное направление горизонтальной оси выберем направление слева направо. Будем перемещать числа внутри строк (при этом в одну клетку могут попадать несколько чисел) и следить за изменением S. Вначале сумма чисел в каждом столбце равна n(n²+1)/2 (1/n от суммы всех чисел, стоящих на доске). В клетку с числом k входит n²–k векторов, а выходит из неё k–1 векторов. Если мы передвинем k на клетку влево, то сумма S меняется на (k–1)–(n²–k)=2k–1–n². Последовательно передвинем n чисел a₁, a₂, …, a_n, которые стояли на одном столбце, на одну клетку влево. При этом S меняется на (2a₁–1–n²)+(2a₂–1–n²)+…+(2a_n–1–n²)=2(a1+a2+…+an)–n–n³=n(n²+1)–n–n³=0. Таким образом, последовательно переместив числа каждого столбца в самый левый столбец, получим, что сумма S не изменилась. Но в конце она равна нулю. S=0.
Ответ: 0.


22. Условие.
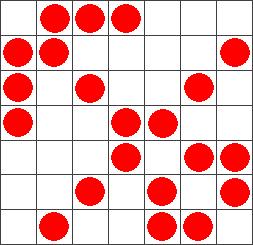
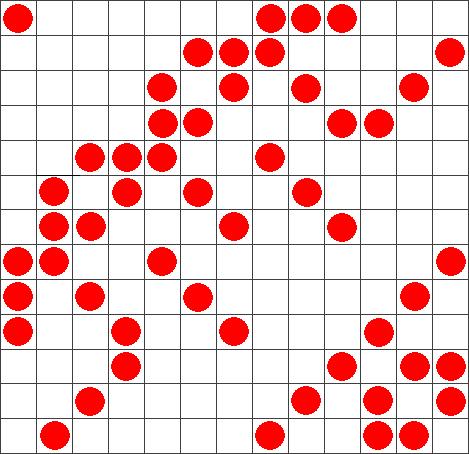
На доске а) 7x7, б)13x13 клеток расставьте наибольшее возможное число шашек так, чтобы никакие 4 из них не являлись вершинами прямоугольника со сторонами, параллельными сторонам доски.
Решение.
Оценим сверху количество шашек, которое можно нужным образом разместить на доске mxm. Пусть x_i – число точек в строке с номером i и x₁+x₂+…+x_m=k. Если в некоторой строке на каких-то двух клетках стоят шашки, то ни в какой другой строке на той же паре клеток шашки стоять не могут. Всего в i-той строке x_i(x_i-1)/2 пар шашек. Так как все пары шашек, то их суммарное число не больше общего числа всевозможных пар, т.е. x₁(x₁-1)/2+...+x_m(x_m-1)/2≤m(m-1)/2. Отсюда x₁²+…+x_m²≤m(m–1)+x₁+…+x_m=m(m–1)+k. Т.к. x₁²+…+x_m²≥(x₁+…+x_m)²/m=k²/m, то k²/m≤m(m–1)+k. Отсюда k≤(m+m√(4m-3))/2.
При m=7 получим k≤21. Пример с расстановкой 21 шашки существует (см. рис.).

При m=13 получим k≤52. Пример с расстановкой 52 шашек существует (см. рис.).

Примеры, реализующие точную оценку, можно строить, например, так:
для доски 7x7: в качестве номеров строк, а также столбцов используем тройки из чисел 0 и 1, отличные от (0; 0; 0). Их как раз 7: (0; 0; 1), (0; 1; 0), (1; 0; 0), (0; 1; 1), (1; 0; 1), (1; 1; 0), (1; 1; 1). На пересечении строки (а₁; а₂; а₃) и столбца (b₁; b₂; b₃) ставим шашку, если а₁b₁+a₂b₂+a₃b₃ чётно;
для доски 13x13: в качестве номеров строк и столбцов используем тройки из чисел 0, 1 и –1, отличные от (0; 0; 0), причём из двух троек, получающихся одна из другой умножением на –1, используется лишь одна. Их как раз 13. На пересечении строки (а₁; а₂; а₃) и столбца (b₁; b₂; b₃) ставим шашку, если а₁b₁+a₂b₂+a₃b₃ делится на 3.